二分查找 | Frank's Blog

一、基本概念

折半查找又称二分查找（Binary Search），它仅适用于有序的顺序表。

折半查找的基本思想是：首先将给定的关键字与表中中间位置的元素比较，若相等，则查找成功，返回该元素的存储位置；若不等，则所需查找的元素只能在中间元素以外的前半部分或后半部分。然后在缩小的范围内继续进行同样的查找，如此重复，直到找到为止，或确定表中没有所需要查找的元素，则查找不成功，返回查找失败的信息。

二、算法实现

二分查找的Java语言实现如下，完整的实现已上传至Gitee，仓库地址：https://gitee.com/fzcoder/data-structure-and-algorithms-demo。

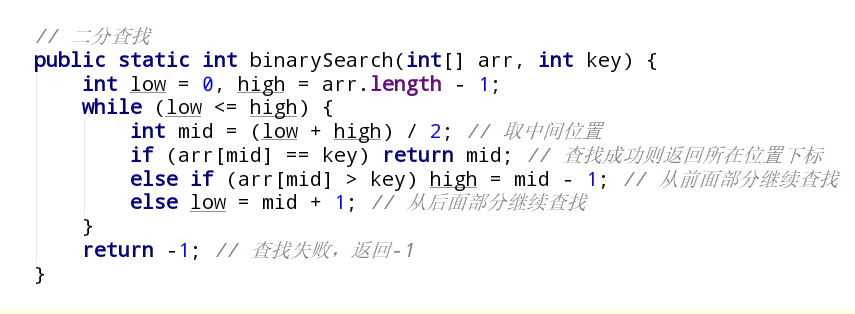
public static int binarySearch(int[] arr, int key) {
    int low = 0, high = arr.length - 1;
    while (low <= high) {
        int mid = (low + high) / 2; // 取中间位置
        if (arr[mid] == key) return mid; // 查找成功则返回所在位置下标
        else if (arr[mid] > key) high = mid - 1; // 从前面部分继续查找
        else low = mid + 1; // 从后面部分继续查找
    }
    return -1; // 查找失败，返回-1
}

注：该算法循环执行的条件是low <= high，而不是low < high，因为low=high时，查找区间还有最后一个结点，还要进一步比较。

下面通过一个例子来说明折半查找算法的执行过程。

假设有一个有序表为：{ 5，16，20，27，30，36，44，55，60，67，71 }，现在要查找值为 27 的数据元素的位置，过程如下：

首先 mid = (1 + 11) / 2 = 6，elem[mid]的值为 36，36 > 27，因此high = mid - 1，即 high = 5。
之后 mid = (1 + 5) / 2 = 3，elem[mid]的值为 20，20 < 27，因此low = mid + 1，即 low = 4。
最后 mid = (4 + 5) / 2 = 4，elem[mid]的值为 27，27 = 27，因此已经找到位置，返回 4。

三、算法分析

上述查找过程的判定树为：

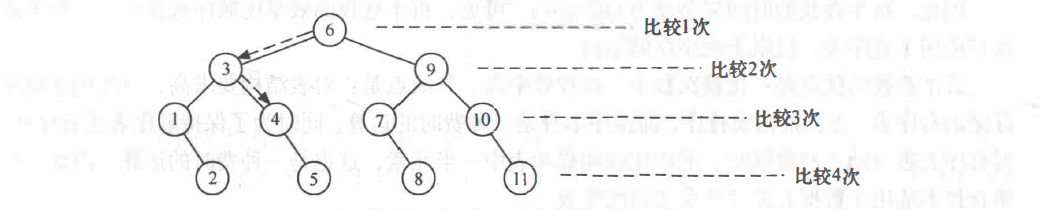
由此可见，折半查找法在查找成功时进行比较的关键字个数最多不超过判定树的深度。而判定树的形态只与表记录个数 n 相关，而与关键字的取值无关。因此，对于长度为 n 的有序表，折半查找法在查找成功时和给定值进行比较的关键字个数至多为：
$$
\lfloor log_2n \rfloor + 1
$$

现在假设如下：

$$
有序表的长度为n = 2^h - 1, 判定树的深度为 h = log_2(n+1)的满二叉树。假设表中每个记录的查找概率相等，均为P_i = \frac{1}{n}
$$

则查找成功时折半查找的平均查找长度为：
$$
ASL = \sum_{i=1}^{n} P_iC_i = \frac{1}{n}\sum_{j=1}^{h}j \cdot 2^{j-1} = \frac{n+1}{n}log_2(n+1)-1
$$
当 n 较大时，可有如下近似结果：
$$
ASL = log_2(n+1)-1
$$
因此，折半查找的时间复杂度为：
$$
T(n)=O(log_2n)
$$
下面来说明折半查找的优点和缺点：