一、插入排序
插入排序是一种简单直观的排序方法,其基本思想是每次将一个待排序的记录按其关键字大小插入前面已排好序的子序列,直到全部记录插入完成。下面将介绍几种常见的插入排序算法。
1、直接插入排序
这是一种最简单的插入排序算法。假设当前索引为 i,在这之前的为有序序列,在这之后的为无序序列,我们要做的就是把当前索引为 i 的元素插入到前面的有序序列中,组成一个新的有序序列,之后将索引向后移动一位,重复上述操作,直到整个序列为有序序列。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
void insert_sort(int* arr, int length)
{
for(int i = 1; i < length; i++)
{
int insert_idx = i-1;
int insert_val = arr[i];
while(insert_idx >= 0 && arr[insert_idx] > insert_val)
{
arr[insert_idx+1] = arr[insert_idx];
insert_idx--;
}
arr[insert_idx + 1] = insert_val;
}
}
|
该算法的时间复杂度为$O(n^2)$,空间复杂度为$O(1)$。
2、折半插入排序
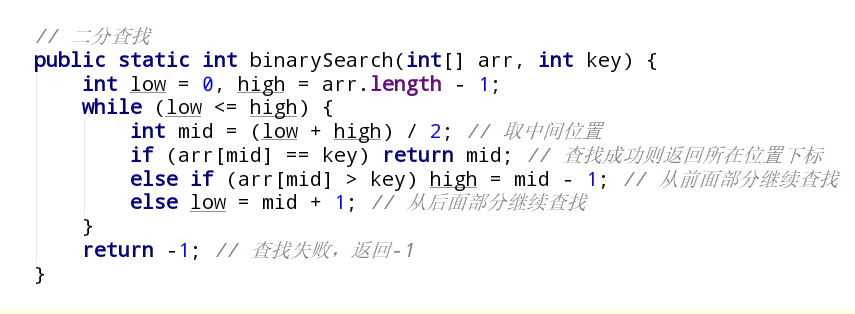
当排序表为顺序表时,可对直接插入排序算法做一些改进,在查找插入位置时使用二分查找,查找完成之后统一地向后移动元素。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| void insert_sort(int* arr, int n) {
int i, j, low, high, mid;
for (i = 2; i <= n; i++) {
arr[0] = arr[i];
low = 1; high = i-1;
while (low <= high) {
mid = (low + high) / 2;
if (arr[mid] > arr[0]) high = mid - 1;
else low = mid + 1;
}
for (j = i - 1; j >= high + 1; --j)
arr[j+1] = arr[j];
arr[high + 1] = arr[0];
}
}
|
该算法的时间复杂度为$O(n^2)$,空间复杂度为$O(1)$。
3、希尔排序
希尔排序(Shell Sort),又称缩小增量排序,是对直接插入排序的一个改进。
交换式算法:
1
2
3
4
5
6
7
8
| void shell_sort(int* arr, int length)
{
for(int gap = length; gap > 0; gap /= 2)
for(int i = gap; i < length; i++)
for(int j = i - gap; j >= 0; j -= gap)
if(arr[j] > arr[j+gap])
swap(&arr[j], &arr[j+gap]);
}
|
如果采用这种写法,排序的效率甚至不如直接插入排序,原因是大量的时间消耗在交换上了。
移动式排序:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| void shell_sort2(int* arr, int length)
{
for(int gap = length; gap > 0; gap /= 2)
{
for(int i = gap; i < length; i++)
{
int j = i;
int tmp = arr[j];
while(j-gap >= 0 && arr[j-gap] > tmp)
{
arr[j] = arr[j-gap];
j -= gap;
}
arr[j] = tmp;
}
}
}
|
二、交换排序
1、冒泡排序
1
2
3
4
5
6
7
8
9
10
11
12
13
| void bubble_sort(int* arr, int length)
{
int i, j;
int tmp;
for(i = 0; i < length - 1; i++)
for(j = 0; j < length - 1 - i; j++)
if (arr[j] > arr[j+1])
{
tmp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = tmp;
}
}
|
该算法的时间复杂度为$O(n^2)$,空间复杂度为$O(1)$。
改进算法:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| void bubble_sort2(int* arr, int length)
{
int i, j;
int tmp;
bool flag = false;
for(i = 0; i < length - 1; i++)
{
for(j = 0; j < length - 1 - i; j++)
if (arr[j] > arr[j+1])
{
flag = true;
tmp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = tmp;
}
if (!flag)
break;
}
}
|
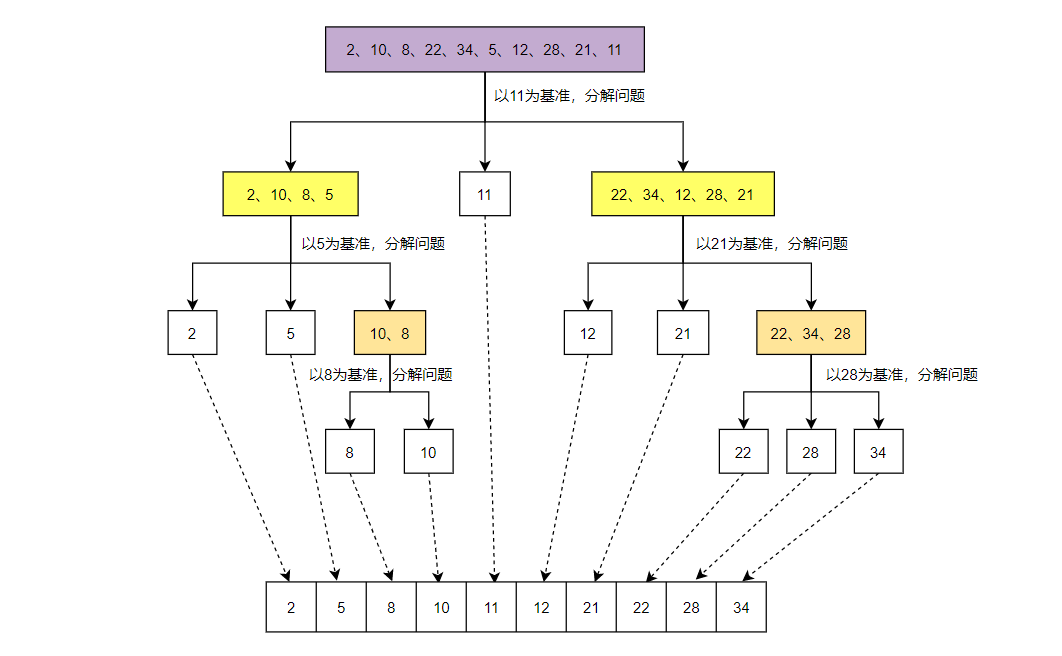
2、快速排序
详见《快速排序》。
三、选择排序
1、简单选择排序
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| void select_sort(int* arr, int length)
{
int i, j;
int min_idx;
for(i = 0; i < length - 1; i++)
{
min_idx = i;
for(j = i + 1; j < length; j++)
if (arr[j] < arr[min_idx])
min_idx = j;
swap(&arr[i], &arr[min_idx]);
}
}
|
该算法的时间复杂度为$O(n^2)$,空间复杂度为$O(1)$。
改进算法:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| void select_sort2(int* arr, int length)
{
int i, j;
int min_idx;
for(i = 0; i < length - 1; i++)
{
min_idx = i;
for(j = i + 1; j < length; j++)
if (arr[j] < arr[min_idx])
min_idx = j;
if (min_idx != i)
swap(&arr[i], &arr[min_idx]);
}
}
|
选择排序的时间要小于冒泡排序。
2、堆排序
详见《堆排序》。
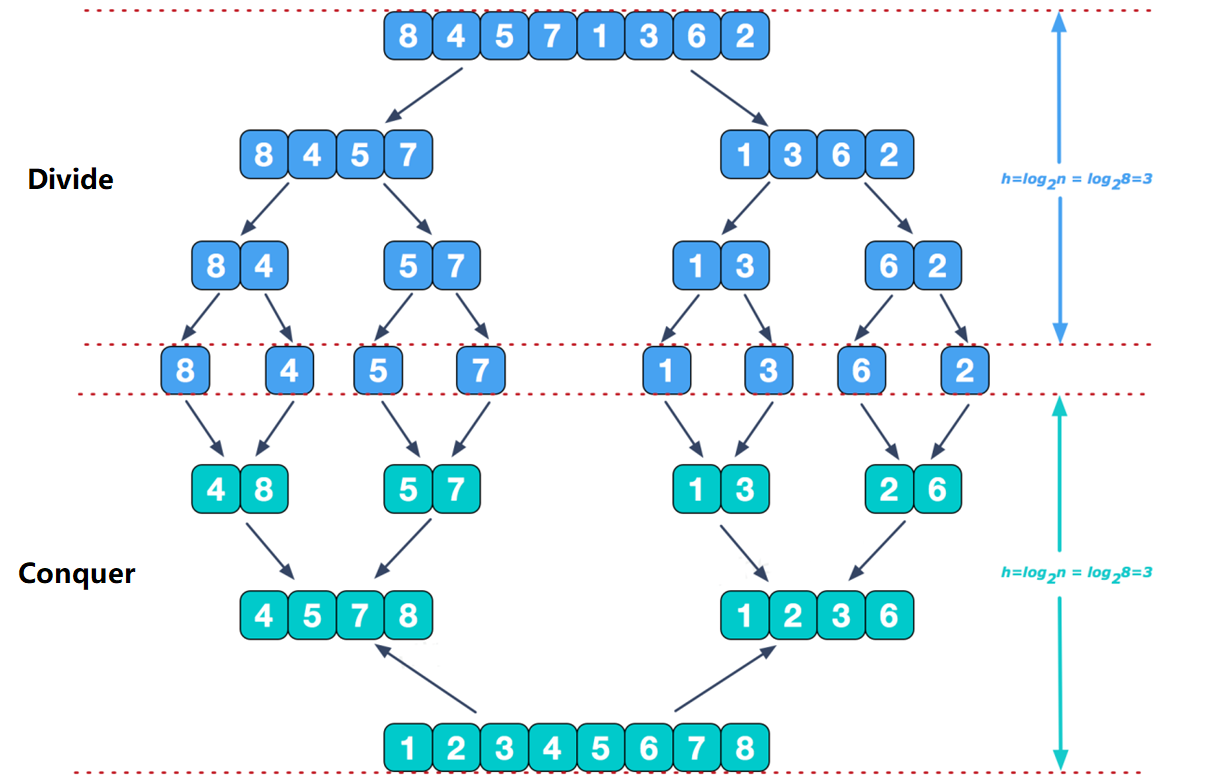
四、归并排序
详见《归并排序》。
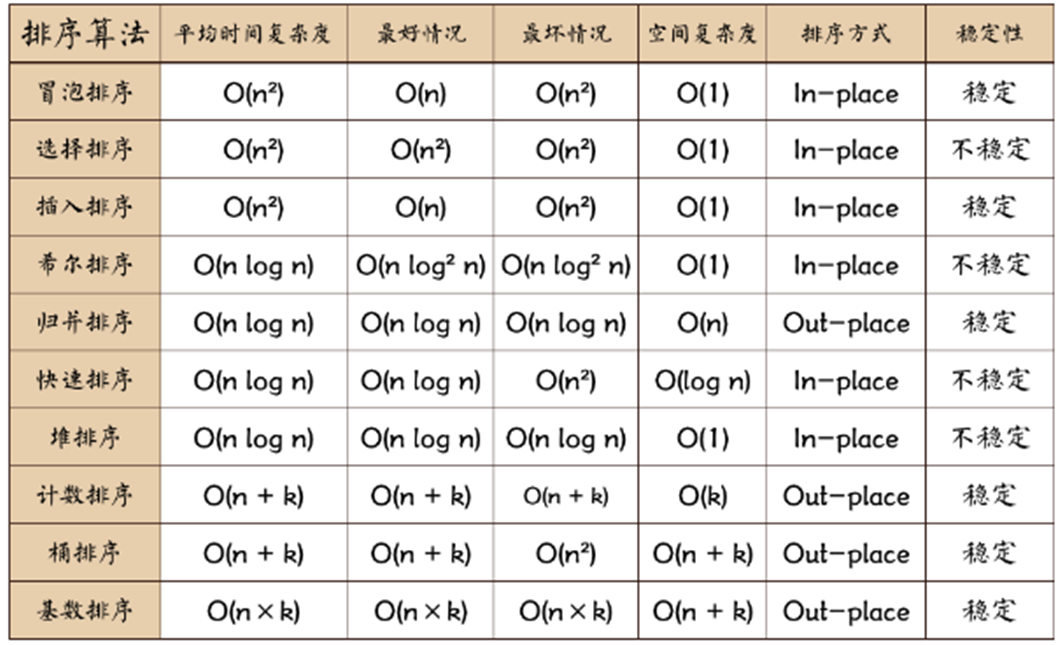
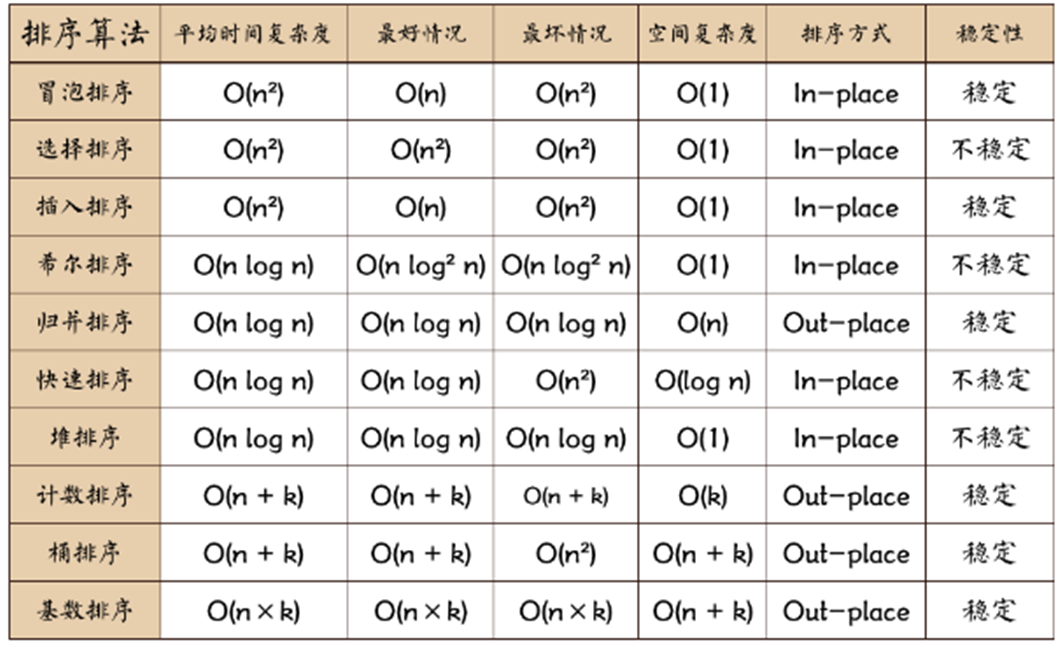
五、排序算法之间的比较