合理地增大校验位、增大码距,能够提高校验码发现错误的能力。因此如果在奇偶校验的基础上增加校验位的位数,构成多组奇偶校验,就能够发现更多位的错误并可自动纠正错误。这就是海明校验码(Hamming Code)的实质所在。
一、基本原理
海明编码的实现原理是:在数据编码中加入几个校验位,并把数据的每一个二进制位分配在几个奇偶校验组中。当某一位出错后,就会引起有关的几个校验组的值发生变化,这样不但可以发现出错,还能指出是哪一位出错。

如果出错代码的位置能够确定,将出错位的内容取反,就能够自动纠正错误,因此满足式(2-14)的海明校验码能够检测出一位错误并且能自动纠正一位错误。
二、编码方式


下面将举一个例子:
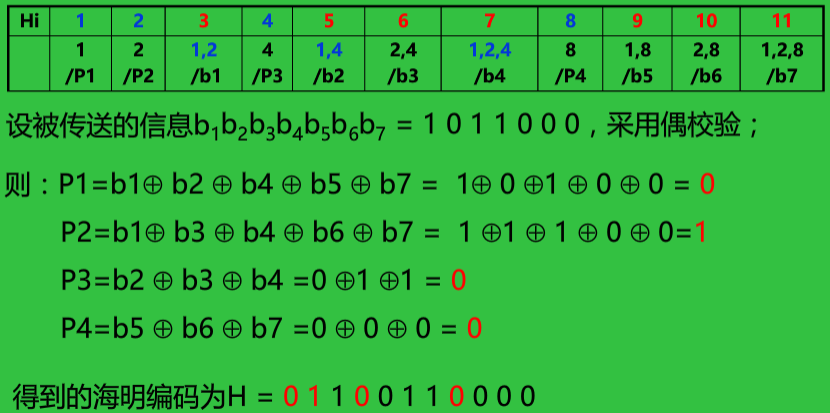
三、校验方式

海明编码的检错需要根据“指错字”的结果进行判断:若“指错字”全为0,则表示信息无误;若“指错字”不全为0,则表示接收到的信息出错,并且“指错字”对应的十进制数就是出错位的位号。
接着举上面的例子:


注意!指错字能够正确指示出错位所在位置的前提是代码中只能有一个错误。如果代码中存在多个错误,就可能查不出来。所以海明校验码只有在代码中只存在一个错误的前提下,才能实现纠错。
下面举个例子:


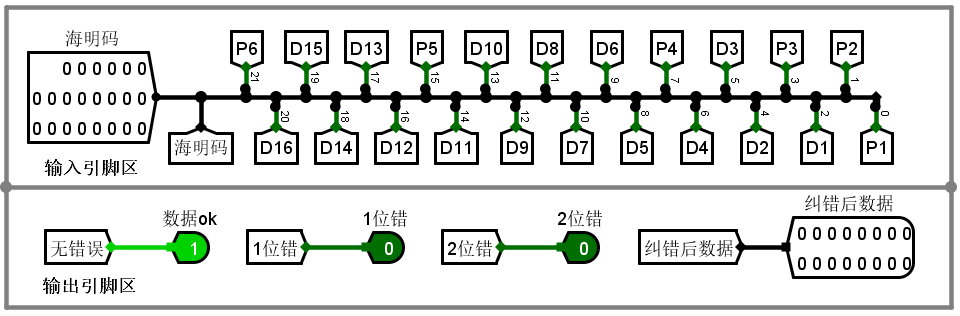
四、海明编码的硬件实现
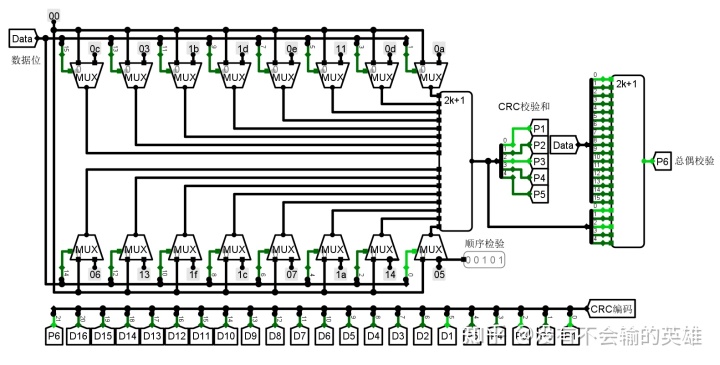
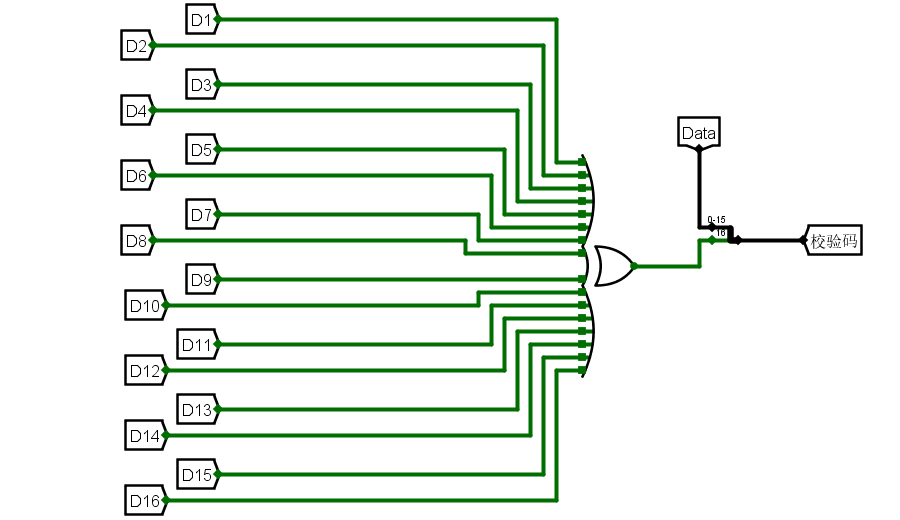
1. 海明编码

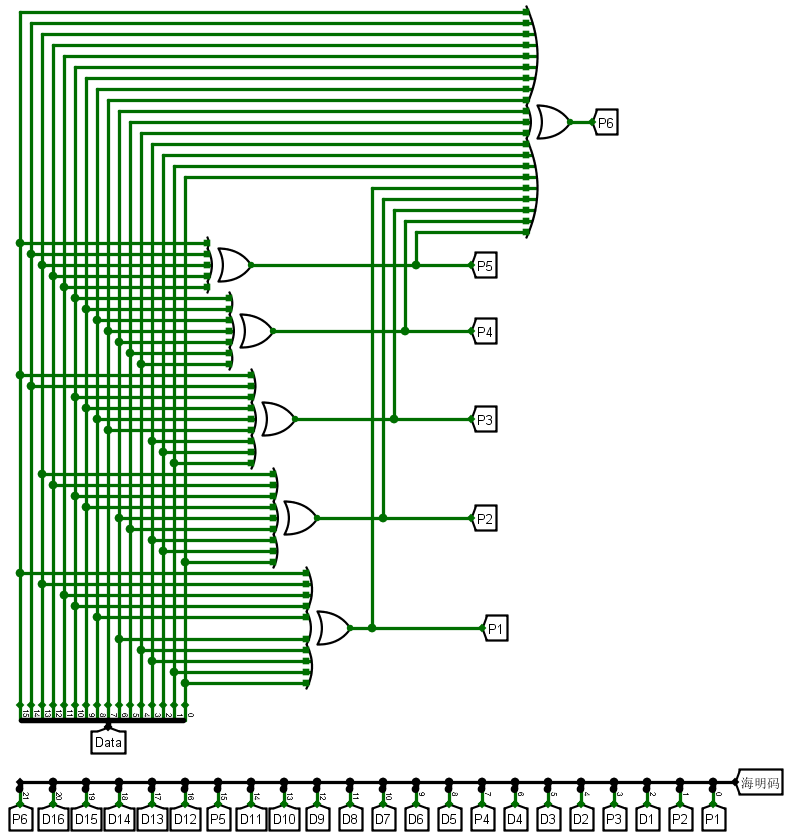
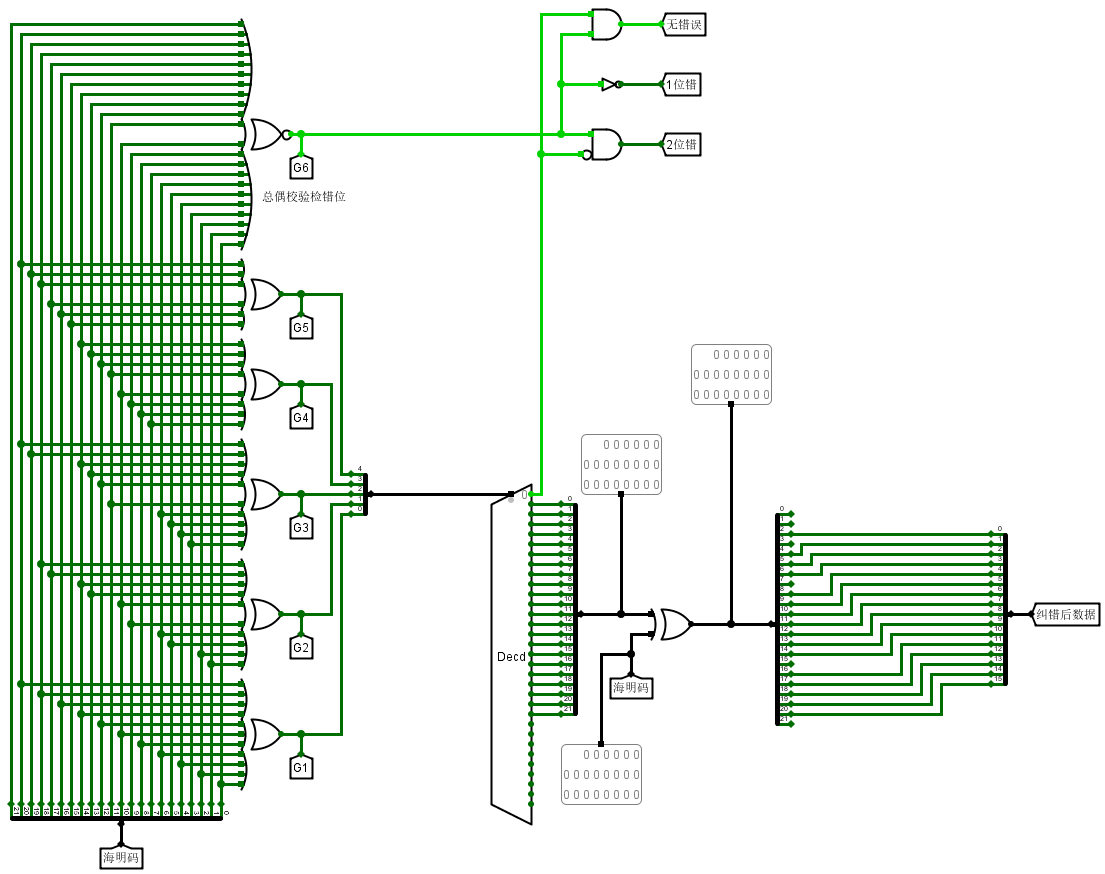
2. 海明解码