一、树
1、基本定义
树(Tree)是 n(n 大于等于 0)个结点的有限集。它或为空树(n = 0),或为非空树(n > 0),对于非空树 T:
- 有且仅有一个称之为根的结点。
- 除根结点以外的其余结点可分为 m(m > 0)个互不相交的有限集 T1,T2,…,Tm,其中每一个集合本身又是一棵树,并称为根的子树。
树具有以下特点:
- 树的根结点没有前驱,除根结点外的所有结点有且仅有一个前驱。
- 树中所有结点可以有零个或多个后继。
2、相关术语
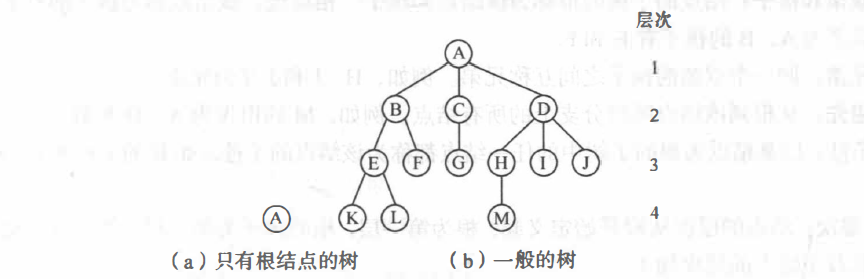
结点:树中的一个独立单元。包含一个数据元素及若干指向其子树的分支,如上图 (b) 中的 A、B、C、D 等。
结点的度:结点拥有的子树数称为结点的度。例如,A 的度为 3,C 的度为 1,, F 的度为 0。
树的度:树的度是树内各结点度的最大值。上图 (b) 所示的树的度为 3。
叶子:度为 0 的结点称为叶子或终端结点。结点 K、L、F、G、M、1、J 都是树的叶子。
双亲和孩子:结点的子树的根称为该结点的孩子,相应地,该结点称为孩子的双亲。例如,B 的双亲为 A,B 的孩子有 E 和 F。
兄弟:同一个双亲的孩子之间互称兄弟。例如,H、I 和 J 互为兄弟。
层次:结点的层次从根开始定义起,根为第一层,根的孩子为第二层。树中任一结点的层次等于其双亲结点的层次加 1。
堂兄弟:双亲在同一层的结点互为堂兄弟。例如,结点 G 与 E、F、H、I. J 互为堂兄弟。
树的深度:树中结点的最大层次称为树的深度或高度。上图 (b) 所示的树的深度为 4。
3、树的性质
树具有如下最基本的性质:
- 树中的结点数等于所有结点的度数之和加 1。
- 度为 m 的树中第 i 层上至多有$m^{i-1}$个结点(i 大于等于 1)。
- 高度为 h 的 m 叉树至多有$(m^h - 1)/(m-1)$个结点。
- 具有 n 个结点的 m 叉树的最小高度为$\lceil log_m(n(m-1) + 1) \rceil$。
二、二叉树
1、基本定义
二叉树(Binary Tree)是 n(n 大于等于 0)个结点的有限集。它或为空树(n = 0),或为非空树(n > 0),对于非空树 T:
- 有且仅有一个称之为根的结点。
- 除根结点以外的其余结点分别为两个互不相交的子集 T1 和 T2,分别称为 T 的左子树和右子树,且 T1 和 T2 本身又都是二叉树。
换句话说,二叉树就是每个结点最多有两个子结点的树。下图将展示二叉树的几种基本形态:

2、特殊的二叉树
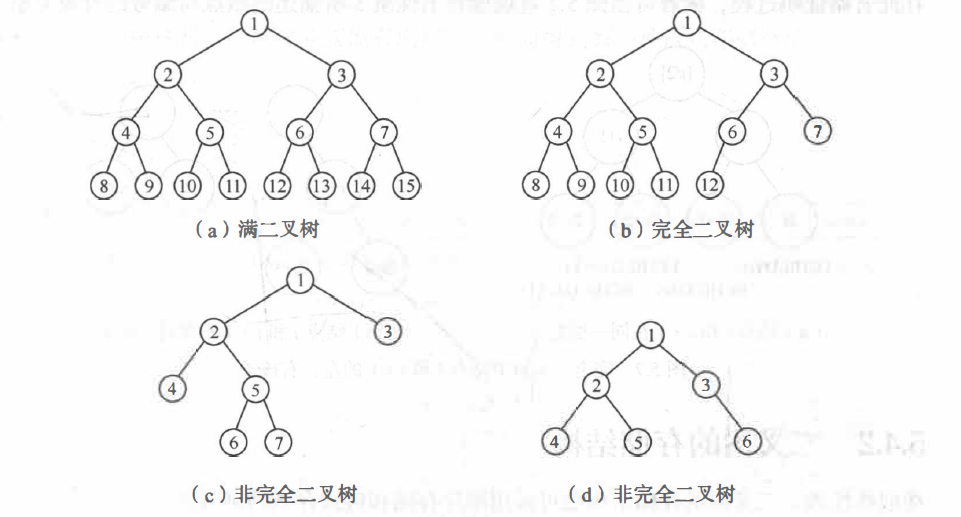
满二叉树:深度为 k 且含有 2^k-1 个结点的二叉树,即树中的每层都含有最多的结点。如下图所示是一棵深度为 4 的满二叉树。
完全二叉树:高度为 h、有 n 个结点的二叉树,当且仅当其每个结点都与高度为 h 的满二叉树中编号为 1~n 的结点一一对应时,称为完全二叉树,如下图所示。

二叉排序树:左子树上所有结点的关键字均小于根结点的关键字;右子树上的所有结点的关键字均大于根结点的关键字;左子树和右子树又各是一颗二叉排序树。
平衡二叉树:树上任一结点的左子树和右子树的深度之差不超过 1。
3、二叉树的性质
非空二叉树上的叶子结点数等于度为 2 的结点数加 1,即 n0 = n2 + 1。
非空二叉树上第 k 层上至多有$2^{k-1}$个结点(k≥1)。
高度为 h 的二叉树至多有$2^h - 1$个结点(h≥1)。
对完全二叉树有如下两条性质:


4、存储结构
(1)顺序存储
顺序存储结构使用一组地址连续的存储单元来存储数据元素,为了能够在存储结构中反映出结点之间的逻辑关系,必须将二叉树中的结点依照一定的规律安排在这组单元中。
对于完全二叉树,只要从根起按层序存储即可,依次自上而下、自左至右存储结点元素,即将完全二叉树上编号为 i 的结点元素存储在如上定义的一维数组中下标为 i-1 的分量中。
对于一般二叉树,则应将其每个结点与完全二叉树上的结点相对照,存储在一维数组的相应分量中,以“0”表示不存在此结点。

由此可见,这种顺序存储结构仅适用于完全二叉树。因为,在最坏的情况下,一个深度为 k 且只有 k 个结点的单支树(树中不存在度为2的结点)却需要长度为 2^k - 1 的一维数组。这造成了存储空间的极大浪费,所以对于一般二叉树,更适合采取下面的链式存储结构。
(2)链式存储
由于顺序存储的空间利用率较低,因此二叉树一般都采用链式存储,用链表结点来存储二叉树中的每个结点。在二叉树中,结点的结构通常包括若干数据域和若干指针域,二叉链表至少包含三个域:数据域、左指针域和右指针域。如下图所示:

用C语言可对二叉树进行如下定义:
1 | typedef struct BiTNode |
三、二叉树的遍历
遍历二叉树(traversing binary tree)是指按某条搜索路径巡访树中每个结点,使得每个结点均被访问一次,而且仅被访问一次。访问的含义很广,可以是对结点做各种处理,包括输出结点的信息,对结点进行运算和修改等。遍历二叉树是二叉树最基本的操作,也是二叉树其他各种操作的基础,遍历的实质是对二叉树进行线性化的过程,即遍历的结果是将非线性结构的树中结点排成一个线性序列。由于二叉树的每个结点都可能有两棵子树,因而需要寻找一种规律,以便使二叉树上的结点能排列在一个线性队列上,从而便于遍历。
遍历二叉树分为三种情况,分别是:先序遍历、中序遍历和后序遍历。例如这里有一个表达式 a + b * (c - d) - e / f 的二叉树:
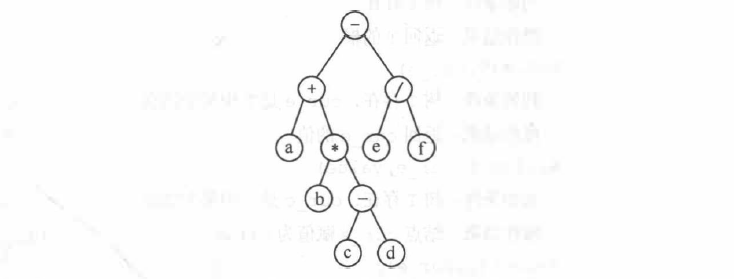
下面将分别介绍三种情况下对该二叉树的遍历结果。
1、先序遍历
先序遍历算法的步骤为:
- 访问根结点
- 先序遍历左子树
- 先序遍历右子树
该算法的实现如下:
1 | void PreOrder(BiTree T) |
采用先序遍历的结果为:- + a * b - c d / e f,该结果即为波兰式。
2、中序遍历
中序遍历算法的步骤为:
- 中序遍历左子树
- 访问根结点
- 中序遍历右子树
该算法的实现如下:
1 | void InOrder(BiTree T) |
采用中序遍历的结果为:a + b * c - d - e / f,该结果即为中缀表达式。
3、后序遍历
后序遍历算法的步骤为:
- 后序遍历左子树
- 后序遍历右子树
- 访问根结点
该算法的实现如下:
1 | void PostOrder(BiTree T) |
采用后序遍历的结果为:a b c d - * + e f / -,该结果即为逆波兰式。
四、线索二叉树
遍历二叉树是以一定规则将二叉树中的结点排列成-一个线性序列,得到二叉树中结点的先序序列、中序序列或后序序列。这实质上是对一个非线性结构进行线性化操作,使每个结点(除第一个和最后一个外)在这些线性序列中有且仅有一个直接前驱和直接后继(在不至于混淆的情况)。
但是,当以二叉链表作为存储结构时,只能找到结点的左、右孩子信息,而不能直接得到结点在任一序列中的前驱和后继信息,这种信息只有在遍历的动态过程中才能得到,为此引人线索二叉树来保存这些在动态过程中得到的有关前驱和后继的信息。
虽然可以在每个结点中增加两个指针域来存放在遍历时得到的有关前驱和后继信息,但这样做使得结构的存储密度大大降低。由于有 n 个结点的二叉链表中必定存在 n+1 个空链域,因此可以充分利用这些空链域来存放结点的前驱和后继信息。试做如下规定:若结点有左子树,则其左指针域指示其左孩子,否则令左指针域指示其前驱;若结点有右子树,则其右指针域指示其右孩子,否则令右指针域指示其后继。为了避免混淆,尚需改变结点结构,增加两个标志域,其结点形式如下图所示。

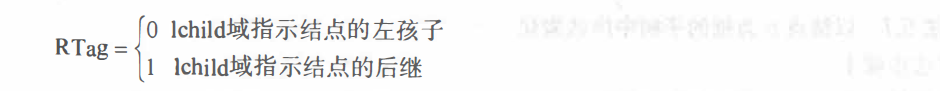
以这种结点结构构成的二叉链表作为二叉树的存储结构,叫做线索链表,其中指向结点前驱和后继的指针,叫做线索。加上线索的二叉树称之为线索二叉树(Threaded Binary Tree)。对二叉树以某种次序遍历使其变为线索二叉树的过程叫做线索化。
五、树和森林
森林是 m (m≥1) 棵互不相交的树的集合。利用孩子兄弟表示法(二叉树表示法)可以实现树和森林的互相转换。
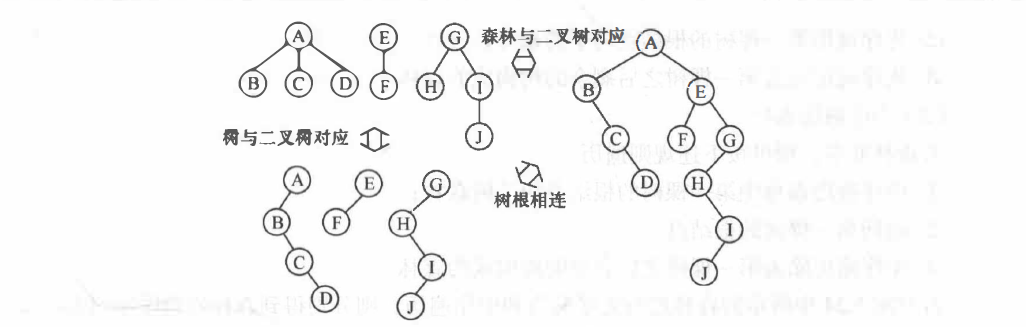
这个一一对应的关系说明森林或树与二叉树可以相互转换。