图

一、图的基本概念

1、基本定义

图（Graph）G 由两个集合 V 和 E 组成，记为 G = ( V, E )，其中 V 是顶点的有穷非空集合，E 是 V 中顶点偶对的有穷集合，这些顶点偶对称为边。V(G )和 E(G) 通常分别表示图 G 的顶点集合和边集合，E(G) 可以为空集。若 E(G) 为空，则图 G 只有顶点而没有边。

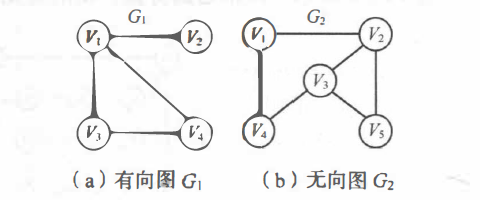
对于图 G，若边集 E(G) 为有向边的集合，则称该图为有向图；若边集 E(G) 为无向边的集合，则称该图为无向图。

2、相关术语

数据结构中图的相关术语与离散数学中的基本相同，这里不再赘述。

二、图的存储结构

1、邻接矩阵

邻接矩阵（Adjacency Matrix）是表示顶点之间相邻关系的矩阵。设 G(V, E) 是具有 n 个顶点的图，则 G 的邻接矩阵是具有如下性质的 n 阶方阵：

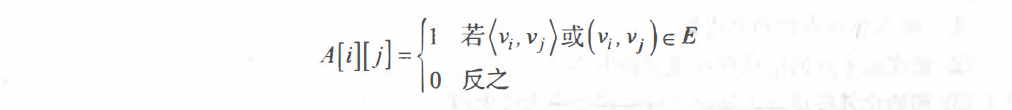
例如本文第一张图中的 G1 和 G2 的邻接矩阵如下所示：

对于带权图来说，若顶点 vi 和 vj 之间有边相连，则邻接矩阵中对应项存放着该边对应的权值，若顶点 Vi 和 Vj 不相连，则用 ∞ 来代表这两个顶点之间不存在边：

其中，Wij表示边上的权值；∞ 表示计算机允许的、大于所有边上权值的数。例如，下图为一个有向网和它的邻接矩阵：

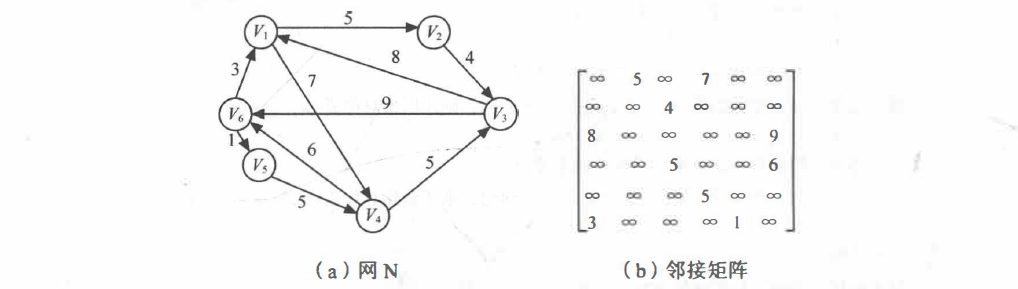
用邻接矩阵表示法表示图，除了一-个用于存储邻接矩阵的二维数组外,还需要用一个一维数组来存储顶点信息。其形式说明如下：

#define MAXINT 0x7FFF // 表示极大值
#define MVNum 100 // 最大顶点数

typedef char VerTexType; // 假设顶点的数据类型为字符型
typedef int ArcType; // 假设边的权值类型为整型

typedef struct
{
    VerTexType vexs[MVNum]; // 顶点表
    ArcType arcs[]; // 邻接矩阵
    int vexnum, arcnum; // 图的当前点数和边数
}AMGraph;

2、邻接表

邻接表（Adjacency List）是图的一种链式存储结构。在邻接表中，对图中每个顶点 Vi 建立一个单链表，把与 Vi 相邻接的顶点放在这个链表中。邻接表中每个单链表的第一个结点存放有关顶点的信息，把这一结点看成链表的表头，其余结点存放有关边的信息，这样邻接表便由两部分组成：表头结点表和边表。

• 表头结点表：由所有表头结点以顺序结构的形式存储，以便可以随机访问任一顶点的边链表。表头结点包括数据域和链域两部分，如下图 (a) 所示。其中，数据域用于存储顶点 Vi 的名称或其他有关信息；链域用于指向链表中第-一个结点（即与顶点 V1 邻接的第一个邻接点）。

• 边表：由表示图中顶点间关系的 2n 个边链表组成。边链表中边结点包括邻接点域、数据域和链域三部分，如下图 (b) 所示。其中，邻接点域指示与顶点 Vi 邻接的点在图中的位置；数据域存储和边相关的信息，如权值等；链域指示与顶点 Vi 邻接的下一条边的结点。

例如，下图 (a) 和 (b) 所示分别为本文第一张图中 G1 和 G2 的邻接表。

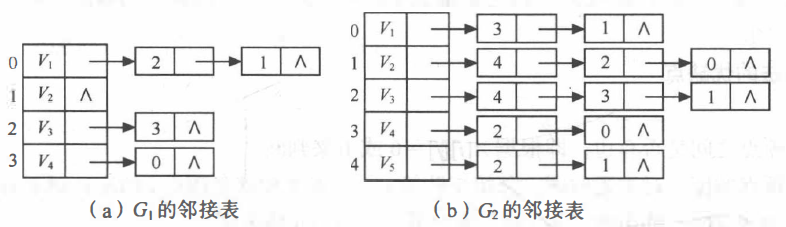
图的邻接表存储结构说明如下：

#define MVNum 100 // 最大顶点数

// 边结点
typedef struct ArcNode
{
    int adjvex; // 该边所指向的顶点的位置
    struct ArcNode* nextarc; // 指向下一条边的指针
    // 其它相关信息
    ...
}ArcNode;

// 顶点信息
typedef struct VNode
{
    VerTexType data;
    ArcNode* firstarc; // 指向第一条依附该顶点的边的指针
}VNode, AdjList[MVNum]; // AdjList 表示邻接表类型

// 邻接表
typedef struct
{
    AdjList vertices;
    int vexnum, arcnum; // 图的当前顶点数和边数
}ALGraph;

三、图的遍历

1、深度优先搜索

（1）简介

深度优先搜索（Depth First Search, DFS）遍历类似于树的先序遍历，是树的先序遍历的推广。对于一个连通图，深度优先搜索遍历的过程如下：

• 从图中某个顶点 v 出发，访问 v。

• 找出刚访问过的顶点的第一个未被访问的邻接点，访问该顶点。以该顶点为新顶点，重复此步骤，直至刚访问过的顶点没有未被访问的邻接点为止。

• 返回前一个访问过的且仍有未被访问的邻接点的顶点，找出该顶点的下一个未被访问的邻接点，访问该顶点。

• 重复步骤 (2) 和 (3)，直至图中所有顶点都被访问过，搜索结束。

以下图 (a) 中所示的无向图 G4 为例，深度优先搜索遍历图的过程如下图 (b) 所示，具体过程如下：

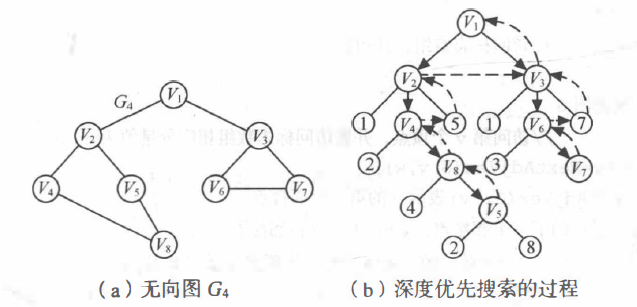
• 从顶点 v1 出发，访问 v1。

• 在访问了顶点 v1 之后，选择第一个未被访问的邻接点 v2，访问 v2。以 v2 为新顶点，重复此步，访问 v4、v8、v5。 在访问了 v5 之后，由于 v5 的邻接点都已被访问，此步结束。

• 搜索从 v5 回到 v8，由于同样的理由，搜索继续回到 v4，v2 直至 v1，此时由于 v1 的另一个邻接点未被访问，则搜索又从 v1 到 v3，再继续进行下去。由此，得到的顶点访向序列为：
  $$
  v_1 \to v_2 \to v_4 \to v_8 \to v_5 \to v_3 \to v_6 \to v_7
  $$

（2）算法实现

深度优先搜索可以通过递归进行实现，算法如下：

bool visited[MVNum]; // 访问标志数组，初值为 false

void DFS(AMGraph G, int v)
{
    // 访问第 v 个结点
    visit(v);
    // 置访问标志数组相应分量值为 true
    visited[v] = true;
    // 依次检查邻接矩阵v所在的行
    for (int w = 0; w < G.vexnum; w++)
        if ((G.arcs[v][w] != 0) && (!visited[w])) // G.arcs[v][w] != 0 表示 w 是 v 的邻接点
            DFS(G, w); // 如果 w 未访问则递归调用DFS（本算法也可以用栈来实现）
}

2、广度优先搜索

（1）简介

广度优先搜索（Breadth First Search, BFS）遍历类似于树的按层次遍历的过程。广度优先搜索遍历的过程如下。

• 从图中某个顶点 v 出发，访问 v。

• 依次访问 v 的各个未曾访问过的邻接点。

• 分别从这些邻接点出发依次访问它们的邻接点，并使“先被访问的顶点的邻接点先于后被访问的顶点的邻接点被访问。重复步骤 (3)，直至图中所有已被访问的顶点的邻接点都被访问到。

例如，对图G4进行广度优先搜索遍历的过程如下图所示：

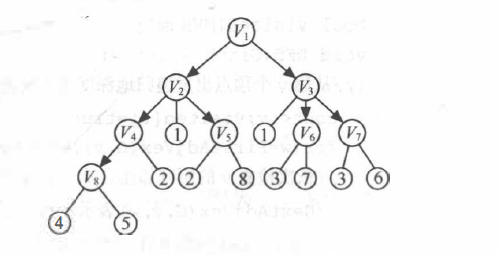
具体过程如下：

• 从顶点 v1 出发，访问 v1。

• 依次访问 v1 的各个未曾访问过的邻接点以和 v3。

• 依次访问 v2 的邻接点 v4 和 v5，以及 v3 的邻接点 v6 和 v7，最后访问 v4 的邻接点 v8。由于这些顶点的邻接点均已被访问，并且图中所有顶点都被访问，由此完成了图的遍历。得到的顶点访问序列为：
  $$
  v_1 \to v_2 \to v_3 \to v_4 \to v_5 \to v_6 \to v_7 \to v_8
  $$

（2）算法实现

广度优先搜索可以通过队列来实现，算法如下：

bool visited[MVNum]; // 访问标志数组，初值为 false

void BFS(AMGraph G, int v)
{
    // 访问第 v 个结点
    visit(v);
    // 置访问标志数组相应分量值为 true
    visited[v] = true;
    // 辅助队列Q初始化
    InitQueue(Q);
    // v 进队
    EnQueue(Q, v);
    // 队列非空
    while(!isEmpty(Q))
    {
        // 队头元素出队并置为u
        DeQueue(Q,u);
        // 依次检查 u 的所有邻接点 w，FirstAdjVex(G,u) 表示 u 的第一个邻接点
        // NextAdjVex(G,u,w) 表示 u 相对于 w 的下一个邻接点，w >= 0 表示存在邻接点
        for(w = FirstAdjVex(G,u); w >= 0; w = NextAdjVex(G,u,w))
            if (!visited[w])
            {
                // 访问w
                visit(w);
                // 置访问标志数组相应分量值为 true
                visited[w] = true;
                // w 入队
                EnQueue(Q,w);
            }
    }
}