一、线性表的基本概念

1、线性表的定义

线性表是具有相同数据类型的 n（n 大于等于 0）个数据元素的有限序列，其中 n 为表长，当 n = 0 时线性表是一个空表。若用 L 命名线性表，则其一般表示为：
$$
L = (a_1, a_2, …, a_i, a_{i+1}, …, a_n)
$$
式中，a1是唯一的“第一个”元素，又称表头元素；an是唯一的“最后一个”数据元素，又称表尾元素。除第一个元素外，每个元素有且仅有一个直接元素。除最后一个元素外，每个元素有且仅有一个直接后继。以上就是线性表的逻辑特性。

由此，我们得出线性表的特点如下：

  • 表中元素的个数有限。
  • 表中元素具有逻辑上的顺序性，有其先后次序。
  • 表中元素都是数据元素，每个元素都是单个元素。
  • 表中元素的数据类型都相同，这意味着每个元素占有相同大小的存储空间。
  • 表中元素具有抽象性，即仅讨论元素间的逻辑关系，而不考虑元素究竟表示什么内容。

注意：线性表是一种逻辑结构，表示元素之间一对一的相邻关系。顺序表和链表是指存储结构，两者属于不同层面的概念。下面通过一张图来说明它们之间的关系：

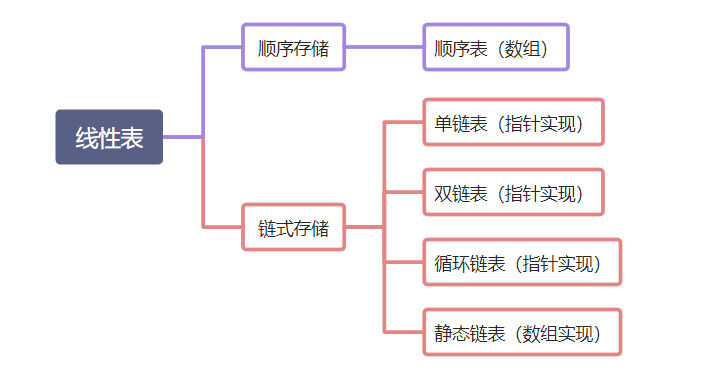
线性表的逻辑结构和存储结构

2、线性表的基本操作

下面通过一张表格来介绍线性表的主要操作：

操作 说明
InitList(&L) 初始化表，构造一个空的线性表
Length(L) 求表长，返回线性表 L 的长度
LocateElem(L, e) 按值查找操作，在表 L 中查找具有给定关键字值的元素
GetElem(L, i) 按位查找操作，获取表 L 中第 i 个位置的元素的值
ListInsert(&L, i, e) 插入操作，在表 L 中的第 i 个位置插入指定元素 e
ListDelete(&L, i, &e) 删除操作，删除表 L 中的第 i 个位置的元素，并用 e 返回删除的元素
PrintList(L) 输出操作，按前后顺序输出线性表 L 的所有元素值
Empty(L) 判空操作，若 L 为空表，则返回true，否则返回false
DestroyList(&L) 销毁操作，销毁线性表，并释放线性表 L 所占用的内存空间

二、顺序表

1、顺序表的定义

线性表的顺序表示指的是用一组地址连续的存储单元依次存储线性表的数据元素，这种表示也称作线性表的顺序存储结构或顺序映像。通常称这种存储结构的线性表为顺序表（Sequential List）。其特点是，逻辑上相邻的数据元素，其物理次序也是相邻的。假设线性表的每个元素需占用 l 个存储单元，并以所占的第一个单元的存储地址作为数据元素的存储起始位置。则线性表中第 i+ 1 个数据元素的存储位置和第 i 个数据元素的存储位置之间满足下列关系：
$$
LOC(a_{i+1}) = LOC(a_i) + l
$$
一般来说，线性表的第 i 个数据元素的存储位置为：
$$
LOC(a_i) = LOC(a_1) + (i-1) \times l
$$
顺序表的存储结构如下图所示：

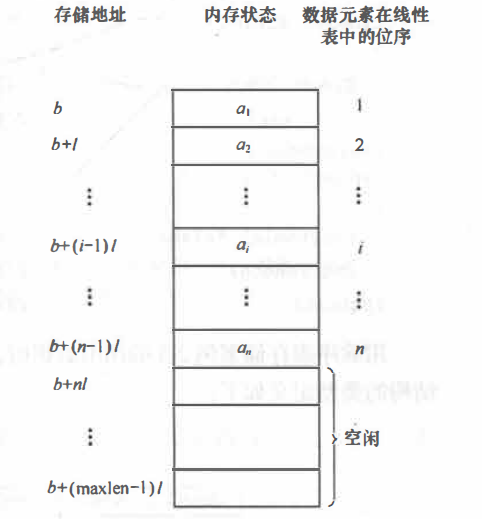
顺序表的存储结构

线性表中的第一个数据元素的存储位置通常称作线性表的起始位置或基地址，又因为线性表的存储空间是连续的，因此只要确定了存储线性表的起始位置，线性表中的任一数据元素都可以随机存取，所以线性表的顺序存储结构是一种随机存取的存储结构。

由于高级程序设计语言中的数组类型也有随机存取的特性，因此，通常都用数组来描述数据结构中的顺序存储结构。例如用 C 语言可对顺序表作如下定义：

1
2
3
4
5
6
7
#define MAXSIZE 100 // 顺序表的最大长度

typedef struct
{
    ElemType data[MAXSIZE]; // 顺序表的元素
    int length; // 顺序表的当前长度
}SqList;

此外也可以通过动态分配的方式来开辟顺序表的存储空间：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
#define MAXSIZE 100 // 顺序表的最大长度

typedef struct
{
    ElemType *data; // 指示动态分配数组的指针
    int length; // 数组的当前长度
}SqList;

int main()
{
    SqList L;
    // 动态分配内存空间
    L.data = (ElemType*)malloc(sizeof(ElemType) * MAXSIZE);
    
    // ...
    
    // 释放动态分配的内存空间
    free(L.data);
    return 0;
}

2、基本操作的实现

这里只介绍比较重要的插入、删除和按值查找操作。

（1）插入操作

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
bool ListInsert(SqList &L, int i, ElemType e)
{
    // 判断 i 的范围是否有效
    if (i < 1 || i > L.length + 1)
        return false;
    
    // 判断存储空间是否已满
    if (L.length >= MAXSIZE)
        return false;
    
    // 将第 i 个元素及之后的元素后移
    for (int j = L.length; j >= i; j--)
        L.data[j] = L.data[j-1];
    
    // 在位置 i 处放入 e
    L.data[i] = e;
    
    // 线性表长度加1
    L.length++;
    
    return true;
}

现在我们来分析一下该算法的时间复杂度：

  • 最好情况：在表尾插入（即 i = n + 1），元素后移语句不执行，时间复杂度为 *O(1)*。

  • 最坏情况：在表头插入（即 i = 1），元素后移语句将执行 n 次，时间复杂度为 *O(n)*。

  • 平均情况：设
    $$
    p_i = \frac{1}{n+1}
    $$
    是在第 i 个位置上插入一个结点的概率，则在长度为 n 的线性表中插入一个结点时，所需移动结点的平均次数为：
    $$
    \sum_{i=1}^{n+1}p_i(n-i+1) = \sum_{i=1}^{n+1}\frac{1}{n+1}(n-i+1) = \frac{1}{n+1}\sum_{i=1}^{n+1}(n-i+1) = \frac{1}{n+1}\frac{n(n+1)}{2} = \frac{n}{2}
    $$
    因此，线性表插入算法的平均时间复杂度为：
    $$
    T(n) = O(n)
    $$

（2）删除操作

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
bool ListDelete(SqList &L, int i, ElemType &e)
{
    // 判断 i 的范围是否有效
    if (i < 1 || i > L.length)
        return false;
    
    // 将被删除的元素赋值给 e
    e = L.data[i-1];
    
    // 将第 i 个位置后的元素前移
    for (int j = i; j < L.length; j++)
        L.data[j-1] = L.data[j];
    
    // 线性表长度减1
    L.length--;
    
    return true;
}

现在我们来分析一下该算法的时间复杂度：

  • 最好情况：删除表尾元素（即 i = n），无需移动元素，时间复杂度为 *O(1)*。

  • 最坏情况：删除表头元素（即 i = 1），需移动除表头元素之外的所有元素，时间复杂度为 *O(n)*。

  • 平均情况：设
    $$
    p_i = \frac{1}{n}
    $$
    是删除第 i 个结点的概率，则在长度为 n 的线性表中删除一个结点时，所需移动结点的平均次数为：
    $$
    \sum_{i=1}^{n}p_i(n-i) = \sum_{i=1}^{n}\frac{1}{n}(n-i) = \frac{1}{n}\sum_{i=1}^{n}(n-i) = \frac{1}{n}\frac{n(n-1)}{2} = \frac{n-1}{2}
    $$
    因此，线性表插入算法的平均时间复杂度为：
    $$
    T(n) = O(n)
    $$

（3）按值查找

1
2
3
4
5
6
7
int LocateElem(SqList L, ElemType e)
{
    for (int i = 0; i < L.length; i++)
        if (L.data[i] == e)
            return i+1; // 下标为 i 的元素值等于 e，返回其位序 i+1
    return -1; // 查找失败
}

现在我们来分析一下该算法的时间复杂度：

  • 最好情况：查找的元素就在表头，仅需比较一次，时间复杂度为 *O(1)*。

  • 最坏情况：查找的元素在表尾（或不存在）时，需要比较 n 次，时间复杂度为 *O(n)*。

  • 平均情况：设
    $$
    p_i = \frac{1}{n}
    $$
    是查找的元素在第 i（1 <= i <= L.length）个位置上的概率，则在长度为 n 的线性表中查找值为 e 的元素所需比较的平均次数为：
    $$
    \sum_{i=1}^{n}p_i \times i = \sum_{i=1}^{n}\frac{1}{n} \times i = \frac{1}{n}\frac{n(n+1)}{2} = \frac{n+1}{2}
    $$
    因此，线性表插入算法的平均时间复杂度为：
    $$
    T(n) = O(n)
    $$

三、链表

1、单链表

（1）单链表的定义

链表是有序的链表，它在内存中的存储结构如下：

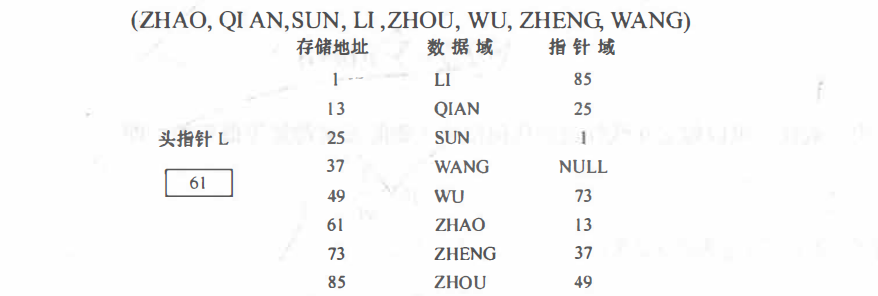
链表的存储结构

通过上图，我们可以发现：

  • 链表是以结点（Node）方式来存储的，属于链式存储。
  • 每个结点包含数据域和指针域，其中数据域用于存放数据，指针域用于指向下一个结点。
  • 链表的各个结点不一定是连续存储的。

为了更好的理解链表，我们通常用下图来表示链表的逻辑结构：

链表的逻辑结构

一般情况下，为了处理方便，在单链表的第一个结点之前附设一个结点，称之为头结点。下图将展示带头结点的链表的逻辑结构：

带头结点的链表

相比于没有头结点的链表，增加了头结点的链表具有以下优点：

  • 便于首元结点的处理。增加了头结点后，首元结点的地址保存在头结点(即其“前驱”结点)的指针域中，则对链表的第一个数据元素的操作与其他数据元素相同，无需进行特殊处理。
  • 便于空表和非空表的统一处理。增加头结点后，无论链表是否为空，头指针都是指向头结点的非空指针，判断是否为空表只需判断头结点的指针域是否为空指针即可。

在 C 语言中，可以通过结构体来定义一个链表的结点：

1
2
3
4
5
typedef struct LNode
{
	ElemType data; // 数据域
    struct LNode *next; //指针域
}LNode, *LinkList;
（2）基本操作的实现

这里仅介绍创建单链表、插入结点和删除结点操作的实现，其它操作如初始化、查找等较为简单，这里不再进行演示。

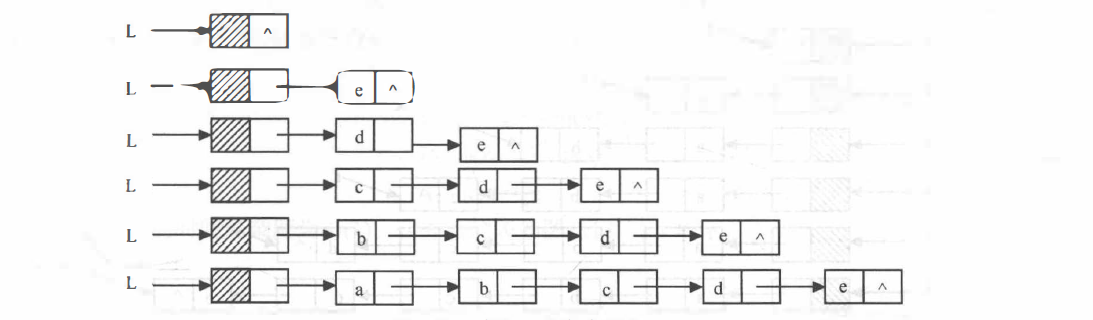
  • 采用头插法建立单链表
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
LinkList HeadInsert(LinkList &L, int n)
{
    int i;
    // 创建一个带头结点的空链表
    L = new LNode;
    L->next = NULL;
    for (i = 0; i < n; i++)
    {
        // 生成新结点
        p = new LNode;
        // 输入元素值赋给新结点的数据域
        cin >> p->data;
        // 将新结点插入到头结点之后
        p->next = L->next;
        L->next = p;
    }
}

该算法实现的效果如下：

头插法

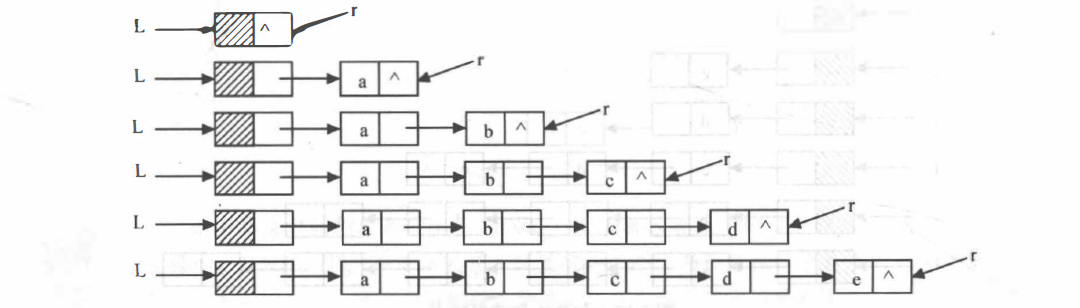
  • 采用尾插法建立单链表
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
LinkList HeadInsert(LinkList &L, int n)
{
    int i;
    // 创建一个带头结点的空链表
    L = new LNode;
    L->next = NULL;
    LinkList q = L;
    for (i = 0; i < n; i++)
    {
        // 生成新结点
        p = new LNode;
        // 输入元素值赋给新结点的数据域
        cin >> p->data;
        // 将新结点插入到尾结点之后
        q->next = p;
        q = q->next;
    }
}

该算法实现的效果如下：

尾插法

  • 插入结点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
bool ListInsert(LinkList &L, int n, ElemType e)
{
    int i = 0;
    LinkList p = L;
    // 1.查找第 n-1 个结点
    while (p && (i < n-1))
    {
        p = p->next;
        i++;
    }
    // i > n+1 或者 i < 1
    if (!p || i > n-1)
        return false;
    // 2.生成新结点
    LinkList s = new LNode;
    // 3.设置数据域
    s->data = e;
    // 4.将结点 s 的指针域指向第 n 个结点
    s->next = p->next;
    // 5.将结点 p 的指针域指向结点 s
    p->next = s;
    return true;
}

该算法实现的效果如下：

插入结点

该算法的时间复杂度为 *O(n)*。

  • 删除结点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
bool ListInsert(LinkList &L, int n, ElemType e)
{
    int i = 0;
    LinkList p = L;
    // 1.查找第 n-1 个结点
    while (p && (i < n-1))
    {
        p = p->next;
        i++;
    }
    // 当 i > n 或 i < 1 时，删除位置不合理
    if (!(p->next) || (i > n-1))
        return false;
    // 临时保存被删除结点的地址以备释放
    LinkList q = p->next;
    // 改变删除结点前驱结点的指针域
    p->next = q->next;
    // 释放删除结点的空间
    delete q;
    return true;
}

该算法实现的效果如下：

删除结点

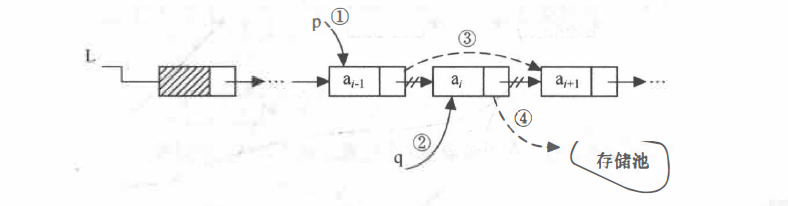
该算法的时间复杂度为 *O(n)*。

2、双链表

单链表的结点中只有一个指示直接后继的指针域，因此从某个结点出发只能顺指针向后寻查其他结点。若要寻查结点的直接前驱，则必须从表头指针出发。换句话说，在单链表中，查找直接后继结点的执行时间为 *O(1)*，而查找直接前驱的执行时间为 *O(n)*。为克服单链表这种单向性的缺点，可利用**双向链表( Double Linked List )**。

顾名思义，在双向链表的结点中有两个指针域，一个指向直接后继，另-个指向直接前驱，在C语言中可描述如下：

1
2
3
4
5
typedef struct DNode
{
    ElemType data; // 数据域
    struct DNode *prior, *next; // 前驱和后继指针
}DNode, *DLinkList;

双链表在单链表的基础上增加了一个指向其前驱的 prior 指针，因此双链表中的按值查找和按位查找的操作与单链表的相同。但双链表在插入和删除操作的实现上与单链表有较大的不同。下面我们将介绍一下双链表的插入和删除操作。

  • 双链表的插入
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
bool ListInsert(DLinkList &L, int i, ElemType e)
{
    DLinkList p = NULL;
    // 在 L 中确定第 i 个元素的位置指针 p
    if (!(p = GetElem(L, i))) // 查找第 i 个元素
        return false; // p 为 NULL 时，第 i 个元素不存在
    // 生成新结点
    DLinkList s = new DNode;
    // 设置数据域
    s->data = e;
    // 将结点 s 插入 L 中
    // 步骤 1
    s->prior = p->prior;
    // 步骤 2
    p->prior->next = s;
    // 步骤 3
    s->next = p;
    // 步骤 4
    p->prior = s;
    return true;
}

该算法实现的效果如下：

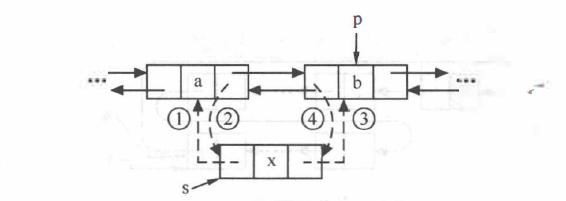
双链表插入

如果不考虑查找结点所消耗的时间，则该算法的时间复杂度为 *O(1)*。

  • 双链表的删除
1
2
3
4
5
6
7
8
9
10
11
12
13
14
bool ListInsert(DLinkList &L, int i, ElemType e)
{
    DLinkList p = NULL;
    // 在 L 中确定第 i 个元素的位置指针 p
    if (!(p = GetElem(L, i))) // 查找第 i 个元素
        return false; // p 为 NULL 时，第 i 个元素不存在
    // 1.修改被删除结点的前驱结点的后继指针
    p->prior->next = p->next;
    // 2.修改被删除结点的后继结点的前驱指针
    p->next->prior = p->prior;
    // 3.释放被删除结点的空间
    delete p;
    return true;
}

该算法实现的效果如下：

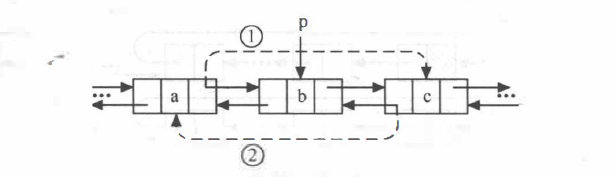
双链表删除

如果不考虑查找结点所消耗的时间，则该算法的时间复杂度为 *O(1)*。

3、循环链表

循环单链表和单链表的区别在于，表中的最后一个结点指针不是NULL，而改为指向头结点，从而整个链表形成一个环，如下图所示：

循环链表

在循环单链表中，表尾结点的指针域指向 L，因此循环单链表判空条件不是头结点的指针是否为空，而是它的指针域是否指向头结点。

循环双链表基本同单链表，不同的是在循环双链表中，头结点的 prior 指针还要指向表尾结点。

4、静态链表

静态链表借助数组来描述线性表的链式存储结构，结点也有数据域和指针域，与一般链表的指针不同的是，这里的指针是结点的相对地址（数组下标），又称游标。和顺序表一样，静态链表也要预先分配一块连续的内存空间。

四、顺序表和链表的区别

1、存取方式

  • 顺序表可以顺序存取，也可以随机存取。
  • 链表只能顺序存取。

2、逻辑结构与物理结构

  • 采用顺序存储时，逻辑上相邻的元素，对应的物理存储位置也相邻。
  • 采用链式存储时，逻辑上相邻的元素，物理位置不一定相邻。

3、查找、插入和删除操作

  • 对于按值查找，顺序表无序时两者的时间复杂度均为 *O(n)*；顺序表有序时可采用二分查找，此时的时间复杂度为：
    $$
    T(n) = O(log_2n)
    $$

  • 对于按序号查找，顺序表的时间复杂度为 *O(1)*，链表的时间复杂度为 *O(n)*。

4、空间分配

  • 顺序表需要预先分配空间，一旦空间装满就无法插入新元素。
  • 链表可以动态分配，只在需要时进行分配即可。

5、存储密度

  • 顺序表的存储密度大。
  • 链表的存储密度相对于顺序表来说较低，因为存在指针域。

五、顺序表 or 链表

顺序表和链表各有其优缺点，那么又该如何选取呢？

  • 难以估计线性表长度的推荐使用链表。
  • 若需要经常访问数据元素推荐使用顺序表。
  • 若需进行频繁的进行插入、删除操作的推荐使用链表。